文章转载自yc97463240,原文链接http://www.useful2you.com/cst-tutorial/
前言:这个教程是在本人时给研究生上课时准备的,主要介绍了CST微波工作室的算法原理、操作流程 ,并进行案例演示和技巧讨论,此处重新整理供大家参考。
 先讲讲CST由来的小故事:CST全称Computer Simulation Technology,是德国教授Prof. Dr.-Ing. Thomas Weiland的杰作,他博士二年级提出了CST核心算法有限积分技术(Finite Integration Technique -FIT,1977年发表[1]),第三年就从达姆施塔特工业大学 (Technische Universität Darmstadt)博士毕业了。
先讲讲CST由来的小故事:CST全称Computer Simulation Technology,是德国教授Prof. Dr.-Ing. Thomas Weiland的杰作,他博士二年级提出了CST核心算法有限积分技术(Finite Integration Technique -FIT,1977年发表[1]),第三年就从达姆施塔特工业大学 (Technische Universität Darmstadt)博士毕业了。

博士毕业后,他先后在德国、美国、日本等多个学校和研究所任职,积累了丰富的科研学术资本后于1989年回到母校,当上了电磁场理论研究所(Theorie Elektromagnetischer Felder)的老大,3年后(博士毕业12年),开了三维电磁仿真软件公司,起名CST (德语Computer-Simulationstechnik)。如今经过了二十多年的发展, CST在电磁仿真领域占据了绝对的统治地位,并于2016年成功被法国达索系统(Dassault Systemes)公司以2.2亿欧元收购,Thomas Weiland教授最终成为名副其实的人生赢家。
(1) 算法介绍
CST软件包含的仿真产品很多,这里仅已微波工作室(MWS)为例进行介绍。与时域有限差分(FDTD)不同,MWS核心算法FIT是对Maxwell积分方程进行离散处理,然而在直角坐标下,FIT与FDTD算法却是等效的[2],因此可以参照FDTD方法的理解来学习FIT算法。
具体来说,首先将计算区域分割成一些列的小立方块,在每个立方块的棱边中心进行电场强度E(x,y,z,t)采样、立方块的面中心进行磁场强度H(x,y,z,t)采样(空间离散 )。如果区域离散足够小,积分方程可近似表达成离散求和的形式,这样方程就可以改写为矩阵形式(注意变量时间偏微分暂时以点帽表示,变量上方加点)。
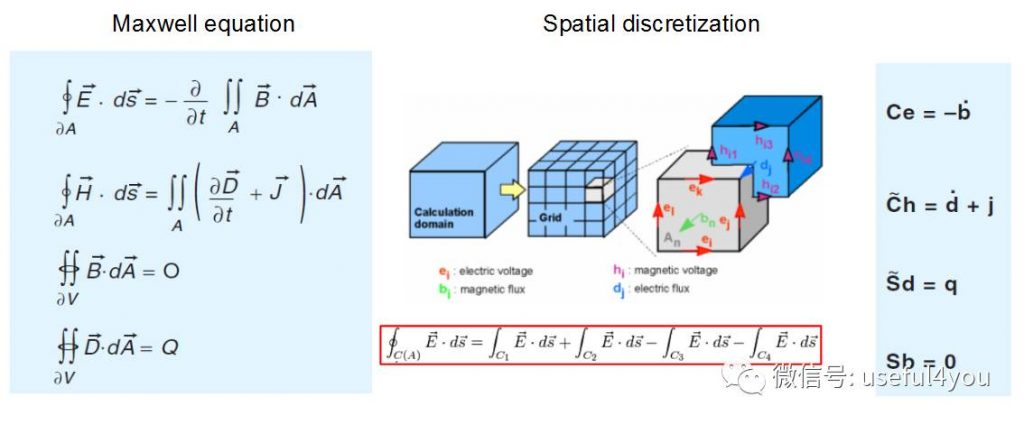
接下来进行时间采样 ,与FDTD一样,将时间偏微分进行差分:对电场强度E和磁感应强度B进行等时间间隔采样,但E和B采样时间点交错半个时间步。对于剩余变量电位移D和磁场强度H则采用本构关系进行表示。

最后,将空间离散和时间采样综合在一起,实现的效果是:指定计算区域空间场的初始状态、电磁激励源以及边界条件,算法可以交替算出电场磁场在各个时间步的值。
这里需要着重指出的是,无论是FIT还是FDTD,时空离散采样是关键!试想一下,如果电场和磁场空间采样位于同一位置、时间采样位于同一时刻,那么离散后的方程组求解将变得异常困难(无解析表达形式,且未知量N多)。而采用时空交错采样的方式,俗称蛙跳式(Leap frog algorithm),离散后的方程组经过简单整理,可直接迭代求解,且方便大规模并行计算 。
此外,关于完整的FIT仿真,还涉及到数值稳定、边界条件、空间场/电路激励以及近远场变换 等诸多内容,需要深入学习的朋友可参考FDTD相关内容(公众号文章我的FDTD学习之路提供相关专题资料分享)。
(2) 仿真流程
总的来说,CST微波工作室仿真流程可分为六步:
1. 初始设置
主要是设置时间/长度单位、背景填充,例如,设置m为长度单位,GHz为频率单位,背景为自由空间。
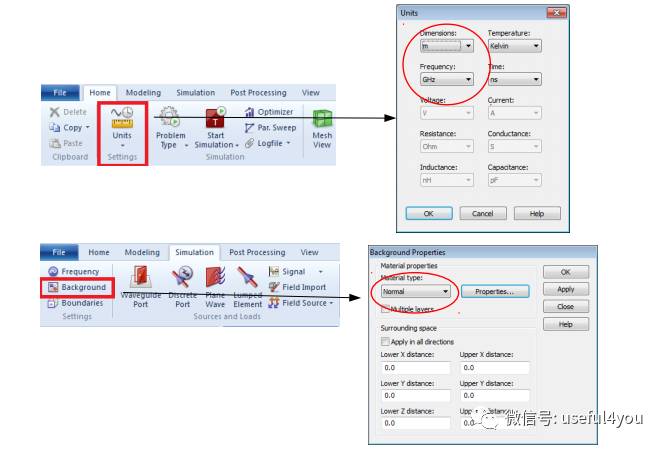
2. 建立模型
CST建模种类齐全、功能完善、操作简单,除了能绘制简单的立方体、球、圆柱、圆锥等模型以外,还可以根据用户的需求进行大量的几何变化,例如拉伸、镂空、平移、组合等等,还支持参数化建模以及外界CAD模型导入。
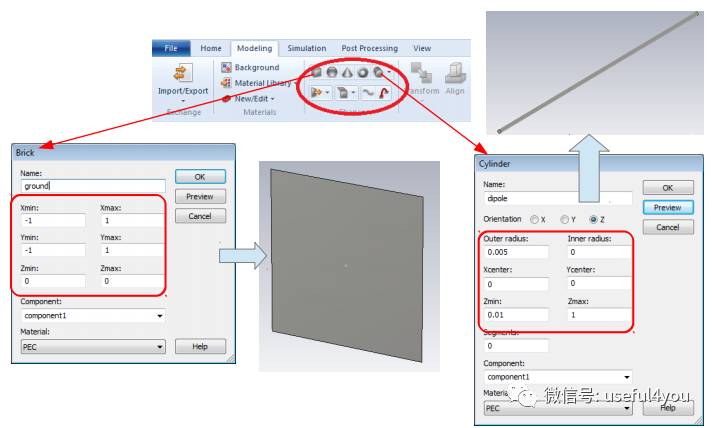
3. 定义激励
对于时域仿真,一般是通过一个宽带高斯脉冲激励,然后得到仿真对象的宽带电磁散射特性,为此需要先设置频率范围,然后设置激励样式,主要包括空间场激励(平面波、近场)和电路激励 (波导、离散端口)。
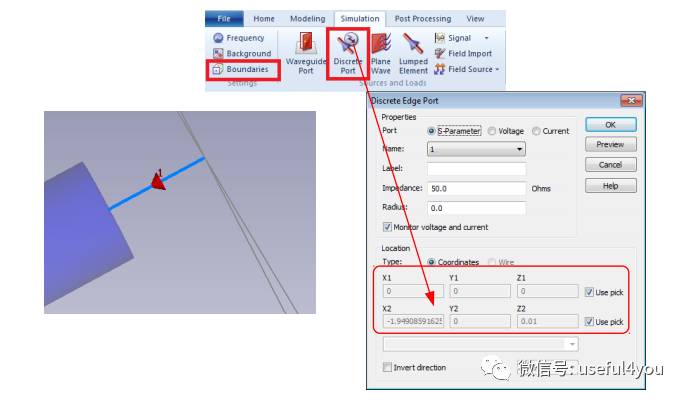
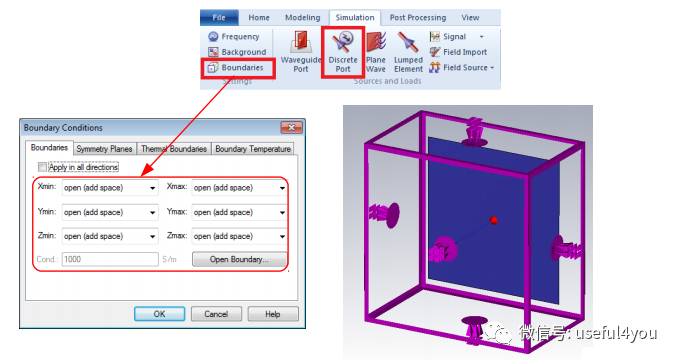
4. 设定边界
由于计算机内存和计算速度有限,必须对仿真区域进行截断,一般有电场 、磁场和吸波 三种边界条件。其中电场边界为切向电场为零,磁场边界为切向磁场为零,吸波边界为电磁波传输无反射,一般通过理想匹配层(PML)实现。**
**
5. 设置监视
由于FIT仿真过程中会产生大量的中间变量,如果全部保存,一方面会耗费大量内存,另一方面会降低计算速度,为此根据后处理需要,仅保留有用的计算结果。例如需要观察某一横截面的电场分布,那么计算过程中会把该横截面每个时间步的电场值记录下来,而不必保留全空间的每时刻电场值。**
**

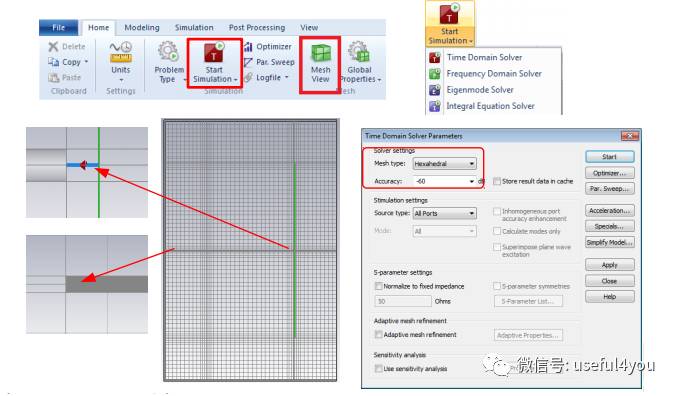
6. 剖分仿真
对于块状均匀物体 来说,计算区域网格剖分密度达到最高频率波长十分之一 时,仿真精度即可得到要求;但如果仿真对象包含细微结构 ,例如单极子天线,那么剖分时必须对细微结构处进行检查,确保离散剖分模型准确描述原有结构的电磁特性,此时网格剖分密度可能低至1/40波长,甚至更低 。
模型剖分完毕,便可进行时域仿真,由于FIT时域求解器是基于时空迭代策略进行的,为此需要人工定义仿真截止条件 ,采用默认设置时表示计算区域场能量耗散至可以忽略的水平时停止计算,用户也可以自定义最大仿真时间进行限制。
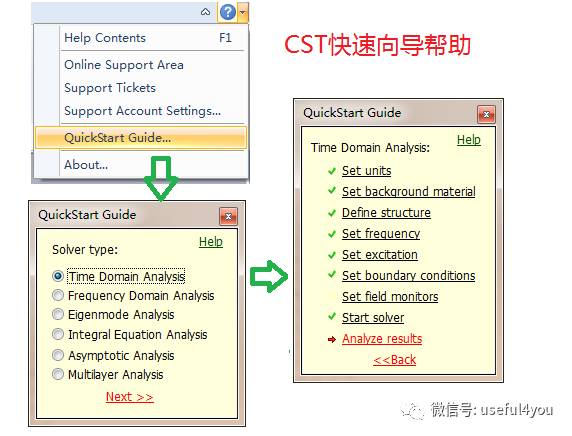
以上是本人从数值计算角度总结的CST操作流程,与CST官方流程稍有差别。如果初学者对操作流程中选项位置不是很熟悉,那么福利来了,CST帮助文件中有一个快速向导 ,选择时域分析后,程序会将自动选择对应菜单,选择对应项,弹出对话框(十分友好的功能),直接设置即可。
(3) 实例演示
1. 单极子天线
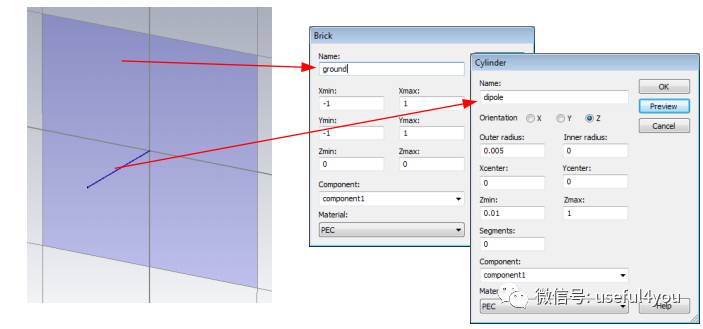
天线仿真建模尺寸
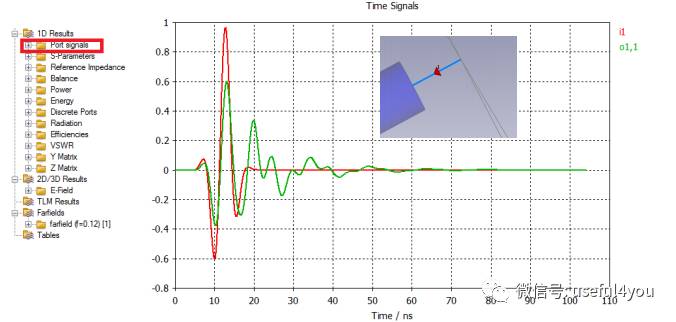
1D结果:馈电端口入射和反射的时域脉冲波形
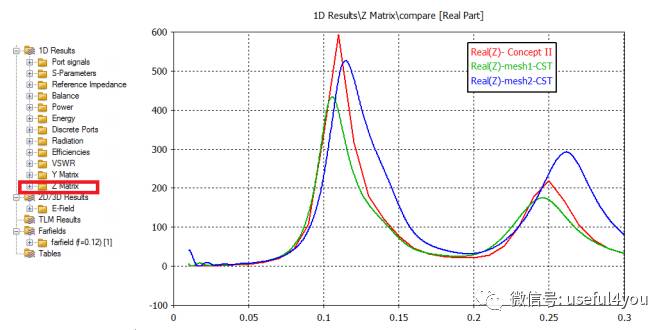
1D结果:输入阻抗随频率的变化
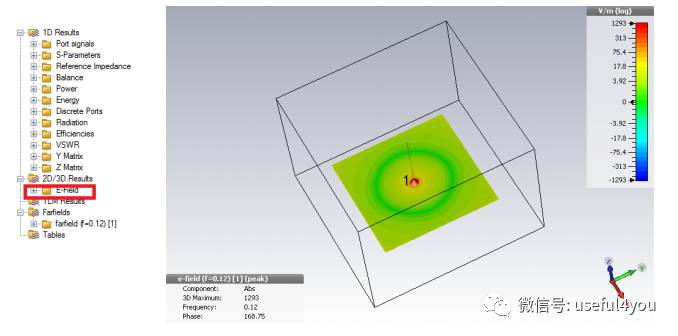
2D结果:二维电场分布
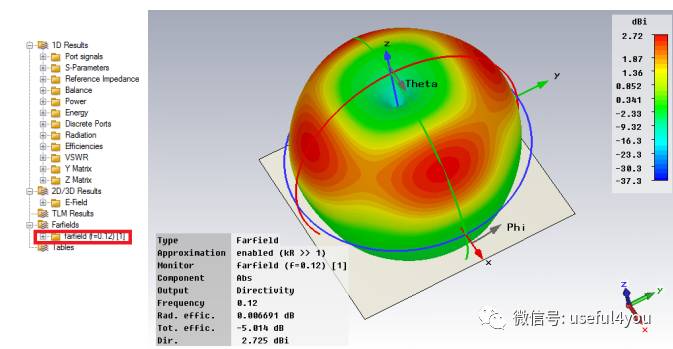
3D结果:远场方向图
2. 贴片天线
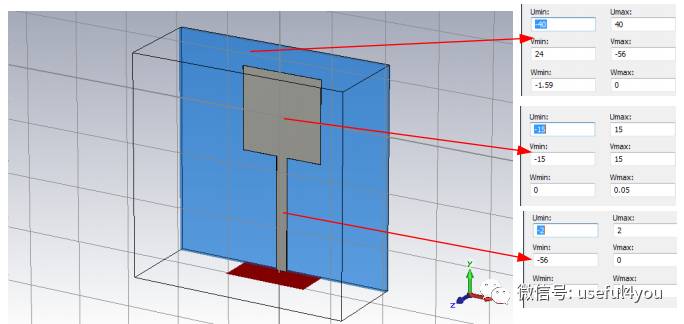
天线仿真建模尺寸
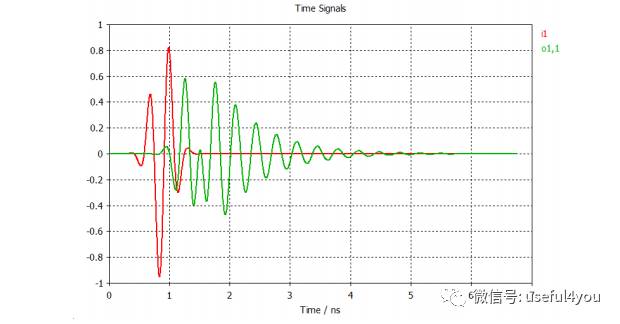
1D结果:馈电端口入射和反射的时域脉冲波形
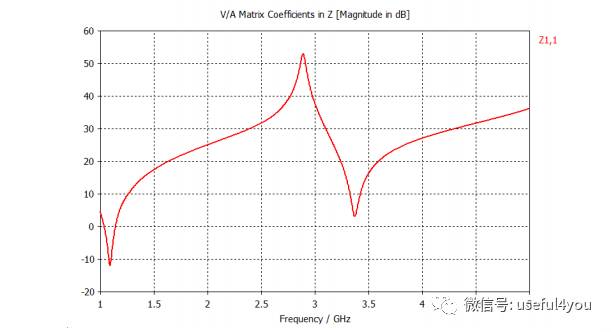
1D结果:输入阻抗随频率的变化
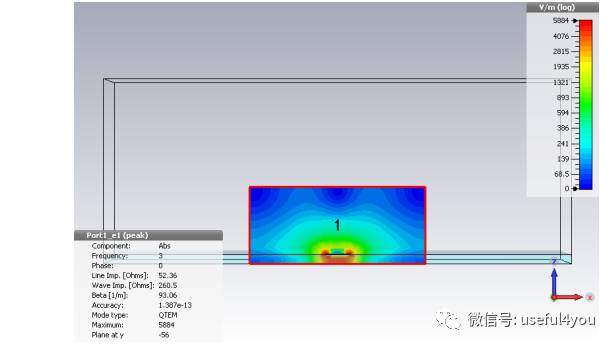
2D结果:二维电场分布
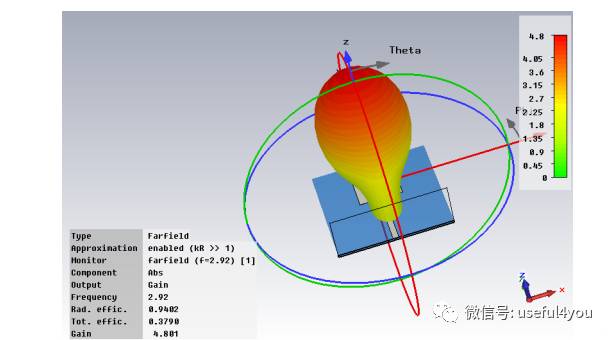
3D结果:远场方向图
(4) 讨论
大多数用户用软件进行仿真的目的是与实测结果进行对比,且习惯性认为,实测结果一定是对的,如果仿真结果不吻合,那就是仿真的问题。个人觉得,无论实验测试还是数值仿真,只有当自己明确自己在干什么时,得到的结果才是可靠的。这就是为什么国外很多电磁计算的大牛几乎一辈子都不用商业软件,而是痴迷并坚信自己的代码 (不是否定商业软件,只是陈述事实)。作为普通的我们,当然没必要这么较真儿,但是从算法和编程的层面加强对仿真软件的后台实现,有百利而无一害!
关于电磁仿真计算,其核心要害在网格剖分 ,网格剖分的好,仿真效率和精度会有显著的提升。
如果仿真对象具有对称性 ,且激励源也处于对称位置,那么恭喜你,可以利用对称边界条件,仿真计算的数据量可成倍降低。
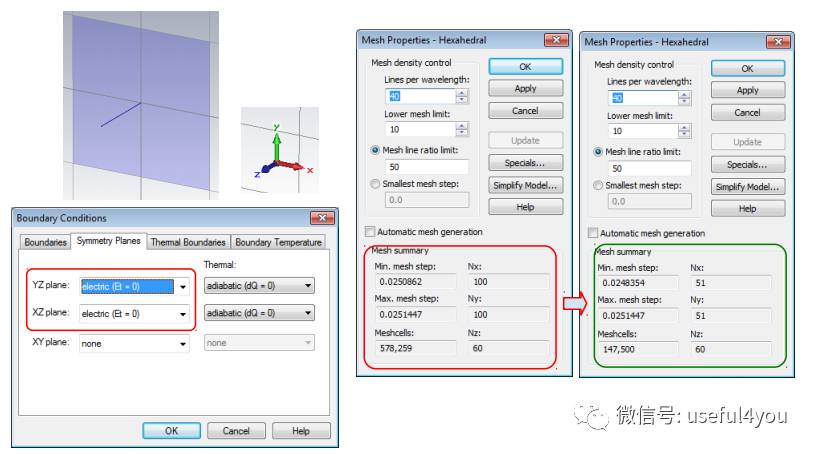
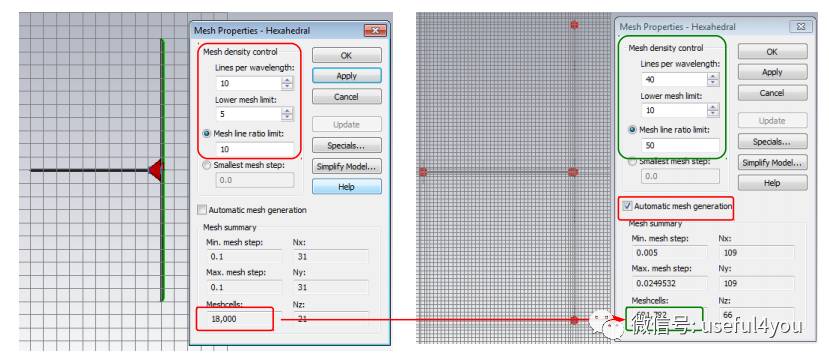
如果仿真对象包含多个部件,且最大尺寸和最小尺寸相差甚远 ,如单极子天线地板和馈源,那么需要引起注意,网格剖分要保证关键部分的细节重现(简单来说,就是用剖分后的网格重新建模,与原有几何模型进行对比),否则稍微加密网格,仿真结果就会发生变化。
总体来说,电磁仿真结果可靠与否,一是通过分析对比,例如与解析结果进行对比,与不同求解器结果进行对比,二是通过实测进行验证。祝大家在今后学习过程中不断加深理解,提高效率。

